visStatistics: The right test, visualised

Sabine Schilling

Institute of Tourism and Mobility, Lucerne University of Applied Sciences and Arts
sabine.schilling@protonmail.com

2025-07-03

library(visStatistics)

Abstract

visStatistics automatically selects and visualises appropriate statistical hypothesis tests between two column vectors of type of class "numeric", "integer", or "factor". The choice of test depends on the class, distribution, and sample size of the vectors, as well as the user-defined ‘conf.level’. The main function visstat() visualises the selected test with appropriate graphs (box plots, bar charts, regression lines with confidence bands, mosaic plots, residual plots, Q-Q plots), annotated with the main test results, including any assumption checks and post-hoc analyses. This scripted workflow is particularly suited for browser-based interfaces that rely on server-side R applications connected to secure databases, where users have no direct access, or for quick data visualisations and test selection, e.g., in statistical consulting projects.

Introduction

While numerous R packages provide statistical testing functionality, few are designed with pedagogical accessibility as a primary concern. The visStatistics package addresses this challenge by automating test selection using deterministic decision logic, removing the burden of manual test choice. This automation enables users to focus directly on interpreting statistical outcomes rather than navigating test selection.

The tailored visual outputs—annotated with test results and, where appropriate, assumption checks and post-hoc analyses—further support comprehension and help ensure valid conclusions from the outset. The package is particularly valuable in statistical consulting for student research projects, where time constraints demand streamlined, assumption-aware output that prioritises interpretation over technical execution. The implemented tests cover the typical content of an introductory undergraduate course in statistics.

The package also suits server-based applications where users have limited interaction: they provide only two input vectors, and the software returns valid, interpretable results without requiring further statistical knowledge. This supports reproducibility and correct inference even in such constrained environments.

The remainder of this vignette is organised as follows:

• Section 3 focuses on the installation and the main function call.

• Section 4 briefly introduces the General Linear Model and the testing of its assumptions in visstatistic.

• Section 5 summarises the decision logic used to select a statistical test.

• Sections 6–8 provide background on the implemented tests and illustrate the decision logic using examples. Function names in parentheses in the headings indicate the corresponding statistical hypothesis test function in R.

• Section 9 outlines the main limitations of the package.

• Section 10 provides an overview of the implemented tests.

Getting started

1. Install the latest development version from GITHUB

install_github("shhschilling/visStatistics")

2. Load the package

library(visStatistics)

3. Minimal function call

The function visstat() accepts input in two ways:

# Standardised form (recommended):
visstat(x, y)

# Backward-compatible form
visstat(dataframe, "namey", "namex")

In the standardised form, x and y must be vectors of class "numeric", "integer", or "factor".

In the backward-compatible form, "namex" and "namey" must be character strings naming columns in dataframe, which must themselves be of class "numeric", "integer", or "factor". This is equivalent to writing:

visstat(dataframe[["namex"]], dataframe[["namey"]])

General Linear Model (GLM)

General Linear Models (GLM) (Searle 1971) provide a unified mathematical framework underlying many common statistical tests like t-tests, ANOVA, and simple linear regression implemented in visStatistics. These tests are not distinct statistical methods, but rather different implementations of the same underlying mathematical framework.

The GLM can be expressed as:

$$Y_i = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_k x_{ik} + \varepsilon_i \quad \text{for } i = 1, \ldots, n, \quad \varepsilon_i \sim {N}(0, \sigma^2)$$

where:

• $n$ = number of observations

• $k$ = number of predictors

• $Y_i$ are the model reandom variables

• $x_{ij}$ are the predictor values

• $\beta_0, \beta_1, \ldots, \beta_k$ are the $(k+1)$ parameters

• $\varepsilon_i$ are the normally distributed error terms with constant, unknwon variance $\sigma^2$

In a more compact matrix for this can be expressed as:

$$\mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}$$

where:

• $\mathbf{Y}$ is $n \times 1$ (response vector for $n$ observations)

• $\mathbf{X}$ is $n \times (k+1)$ (design matrix: $n$ observations, $k+1$ parameters)

• $\boldsymbol{\beta}$ is $(k+1) \times 1$ (parameter vector: $k$ predictors + intercept)

• $\boldsymbol{\varepsilon}$ is $n \times 1$ (error vector for $n$ observations)

Both the paramater and error vector have to be estimated from data:

We observe realisations $y_i$ of the response, and estimate the unknown parameters $\beta_0, \dots, \beta_k$ by minimising the residual sum of squares:

$$\sum_{i=1}^{n} e_i^2 = \sum_{i=1}^{n} \left[y_i - (b_0 + b_1 x_{i1} + \cdots + b_k x_{ik})\right]^2$$

where $b_0, \dots, b_k$ are the least-squares estimators of the true parameters $\beta_0, \dots, \beta_k$.

The fitted value for observation $i$ is

$$\hat{y}_i = b_0 + b_1 x_{i1} + \dots + b_k x_{ik},$$

and the residual is defined as

$$e_i = y_i - \hat{y}_i.$$

The residuals are our estimators for the unknwon error terms $\epsilon_i$. We estimate the unknown variance of the error term by the square standard error

$$s_E^2=1/(n-k-1)⋅\sum_{i=1}^n e_i^2$$

GLM Assumptions and Testing (vis_anova_assumptions())

The GLM assumptions are:

• Linearity: The mean structure $E[\mathbf{Y}] = \mathbf{X}\boldsymbol{\beta}$ is linear in parameters; assessed by checking for systematic patterns in residual plots

Error terms are:

• independent:

• normaliy distributed

• homoscedastic: Constant error variance $\sigma^2$

Assumption Testing in visStatistics

The function vis_anova_assumptions() provides unified diagnostic tools for all GLM variants. Since t-tests, ANOVA, and linear regression share identical distributional assumptions, the same residual-based diagnostics apply universally.

Normality Assessment: The function evaluates residual normality using both the Shapiro-Wilk test (shapiro.test()) and Anderson-Darling test (ad.test()) (Gross and Ligges 2015). These tests offer complementary strengths: Shapiro-Wilk generally exhibits greater power across non-normal distributions in small samples, while Anderson-Darling is highly sensitive to tail deviations in larger samples (Razali and Wah 2011; Yap and Sim 2011).

Homoscedasticity Assessment: Variance equality is tested using the Levene-Brown-Forsythe test (levene.test()) (Brown and Forsythe 1974) and Bartlett’s test (bartlett.test()). The Levene-Brown-Forsythe test uses absolute deviations from group medians, making it robust to non-normality, while Bartlett’s test has greater power when normality holds (Allingham and Rayner 2012).

Visual Diagnostics: visStatistics produces diagnostic plots including: (1) histogram of standardized residuals with normal overlay, (2) residuals vs. fitted values plot, and (3) Q-Q plot. Since algorithmic logic cannot replace expert visual judgment, these plots complement formal tests for comprehensive assumption assessment.

This unified approach eliminates the need to learn separate assumption-checking procedures for each statistical test - they are fundamentally the same method with different design matrices.

The function vis_anvaa_assumption() checks the normality of the standardized residuals by providing diagnostic plots (Q-Q plots, residual vs. fitted values and histograms of residuals ) alongside formal tests (Shapiro-Wilk, Anderson-Darling for testing the normality of the residuals.

For testing homoscedacity), Levene-Test and Bartlett test or testing homoscedacity) help users assess whether the assumptions of the GLM are reasonably met.

Normality of residuals (shapiro.test() and ad.test())

The vis_anova_assumptions() function evaluates the normality of standardised residuals from the aov()-model (which itself is a wrapper function for categorical features around the lm() function) using both the Shapiro–Wilk test (shapiro.test()) and the Anderson–Darling test (ad.test())(Gross and Ligges 2015). These tests offer complementary strengths: Shapiro–Wilk generally exhibits greater power across a range of non-normal distributions in small samples, whereas Anderson–Darling is highly sensitive to tail deviations and performs reliably in larger samples (Razali and Wah 2011; Yap and Sim 2011).

Assessing assumptions solely through p-values can lead to both type I errors (false positives) and type II errors (false negatives). In large samples, even minor, random deviations from the null hypothesis—such as the assumption of normality—can result in statistically significant p-values, leading to type I errors. Conversely, in small samples, substantial violations of the assumption may not reach statistical significance, resulting in type II errors (Kozak and Piepho 2018).

Thus, the robustness of statistical tests depends on both the sample size and the shape of the underlying distribution. This is evident in the limitations of the normality tests used: for instance, the Shapiro–Wilk test is unreliable for large samples ($N > 5000$), while the Anderson–Darling test requires at least 7 observations.

Moreover, assumption tests provide no information on the nature of deviations from the expected distribution (Shatz 2024). Therefore, the assessment of normality should not rely solely on p-values but should be complemented by visual inspection. visstat() produces diagnostic plots including: (1) a histogram of the standardised residuals overlaid with the standard normal distribution, (2) a scatter plot of the standardised residuals versus the fitted values for each predictor level, and (3) a Q–Q plot of the residuals.

Since algorithmic logic cannot replace the combination of formal tests and expert visual judgement, the function defaults to assuming normality if the Shapiro–Wilk test yields a p-value greater than alpha. Simulation studies suggest that Shapiro–Wilk has the highest power among normality tests in small to moderate samples (Razali and Wah 2011).

Equal variances across groups (levene.test() and bartxt.test())

Both aov() and oneway.test() assess whether two or more samples drawn from normal distributions have the same mean. While aov() assumes homogeneity of variances across groups, oneway.test() does not require equal variances.

The decision logic of visStatistics assumes homogeneity of variances if the Levene–Brown–Forsythe test (implemented as levene.test()) (Brown and Forsythe 1974) yields a p-value greater than $\alpha$.

The Levene–Brown–Forsythe test evaluates the null hypothesis that all groups have equal variances by testing whether the absolute deviations from group medians are equal across groups.

For each observation $y_{ij}$ in group $i$, it computes the absolute deviation from the group median:

$$z_{ij} = |y_{ij} - \tilde{y_i}|$$,

where $\tilde{y_i}$ is the median of group $i$.

The test statistic is the F-statistic from a one-way ANOVA on the $z_{ij}$ values:

$$F = \frac{\frac{\sum_{i=1}^{k} n_i (\bar{z}_i - \bar{z})^2}{k-1}}{\frac{\sum_{i=1}^{k} \sum_{j=1}^{n_i} (z_{ij} - \bar{z}_i)^2}{N-k}} = \frac{(N-k) \sum_{i=1}^{k} n_i (\bar{z}_i - \bar{z})^2}{(k-1) \sum_{i=1}^{k} \sum_{j=1}^{n_i} (z_{ij} - \bar{z}_i)^2}$$

where $k$ is the number of groups, $N$ is the total sample size, $n_i$ is the sample size of group $i$, $\bar{z}_i$ is the mean of absolute deviations from the median in group $i$, and $\bar{z}$ is the overall mean of all absolute deviations.

Under the null hypothesis of equal variances, the test statistic follows an F-distribution: $F \sim F(k-1, N-k)$.

The Levene–Brown–Forsythe test improves upon Levene’s original test (Levene 1960) by using the median instead of the mean to centre the data. This makes it more robust to skewed data or data with outliers providing more reliable results in many practical situations. Note that levene.test() mimics the default behaviour of leveneTest() in the car package (Fox and Weisberg 2019).

Additionally, homoscedasticity is assessed via Bartlett’s test (bartlett.test()), which has more power than the Brown–Forsythe version of Levene’s test (Brown and Forsythe 1974) when the normality assumption is met (Allingham and Rayner 2012)

Bartlett’s test evaluates whether sample variances are equal across $k$ normally distributed groups. The test statistic is

$$K^2 = \frac{(N - k) \ln s_p^2 - \sum_{i=1}^k (n_i - 1) \ln s_i^2}{ 1 + \frac{1}{3(k - 1)} \left( \sum_{i=1}^k \frac{1}{n_i - 1} - \frac{1}{N - k} \right)},$$

where $s_i^2$ is the sample variance of group $i$, and $s_p^2$ is the pooled variance:

$$s_p^2 = \frac{1}{N - k} \sum_{i=1}^k (n_i - 1) s_i^2.$$

Under the null hypothesis that all group variances are equal and the data are normally distributed, the test statistic approximately follows a $\chi^2$-distribution with $k - 1$ degrees of freedom (Bartlett 1937).

Decision logic

Throughout the remainder, data of class "numeric" or "integer" are referred to by their common mode numeric, while data of class "factor" are referred to as categorical. The significance level $\alpha$, used throughout for hypothesis testing, is defined as 1 - conf.level, where conf.level is a user-controllable argument (defaulting to 0.95).

The choice of statistical tests performed by the function visstat() depends on whether the data are numeric or categorical, the number of levels in the categorical variable, the distribution of the data, as well as the user-defined ‘conf.level’.

The function prioritizes interpretable visual output and tests that remain valid under the following decision logic:

Numeric response and categorical predictor: Comparing groups

When the response is numeric and the predictor is categorical, a statistical hypothesis test comparing groups is selected.

• If the categorical predictor has exactly two levels, Welch’s t-test (t.test()) is applied when both groups contain more than 30 observations. This heuristic is based on the central limit theorem, which ensures approximate normality of the sampling distribution of the mean (Rasch, Kubinger, and Moder 2011; Lumley et al. 2002; Kwak and Kim 2017). Welch’s t-test is the default method in R for comparing means and is generally preferred over Student’s t-test because it does not assume equal variances. It maintains comparable power even when variances are equal and outperforms Student’s test when variances differ (Moser and Stevens 1992; Fagerland and Sandvik 2009; Delacre, Lakens, and Leys 2017).

• For smaller samples, group-wise normality is assessed using the Shapiro-Wilk test [SHAPIRO and WILK (1965) (shapiro.test()) at a significance level $\alpha$. Simulation studies show that the Shapiro-Wilk test is the most powerful for detecting non-normality across most distributions, especially with smaller sample sizes.(Razali and Wah 2011; Ghasemi and Zahediasl 2012) If both groups are found to be approximately normally distributed according to the Shapiro–Wilk test, Welch’s t-test is applied; otherwise, the Wilcoxon rank-sum test (wilcox.test()) is used.

• For predictors with more than two levels, a model of Fisher’s one-way analysis of variables (ANOVA) (aov()) is initially fitted. The normality of residuals is evaluated by the Shapiro-Wilk test (shapiro.test()); residuals are considered approximately normal if it yields a result exceeding the significance threshold $\alpha$. If this condition is met, the Levene–Brown–Forsythe test (implemented as levene.test()) (Brown and Forsythe 1974) assesses homoscedasticity. When variances are homogeneous ($p > \alpha$), Fisher’s one-way ANOVA (aov()) is applied with Tukey’s Honestly Significant Differences (HSD) (TukeyHSD()) for post-hoc comparison. If variances differ significantly ($p \le \alpha$), Welch’s heteroscedastic one-way ANOVA (oneway.test()) is used, also followed by Tukey’s HSD. If residuals are not normally distributed according to both tests ($p \le \alpha$), the Kruskal–Wallis test (kruskal.test()) is selected, followed by pairwise Wilcoxon tests (pairwise.wilcox.test()). A graphical overview of the decision logic used is provided in the figure below.

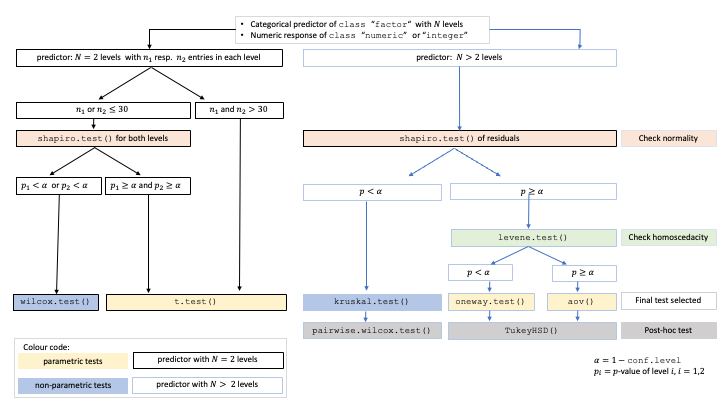
Decision tree used to select the appropriate statistical test for a categorical predictor and numeric response, based on the number of factor levels, normality, and homoscedasticity.

Numeric response and numeric predictor: Simple linear regression

When both the response and predictor are numeric, a simple linear regression model (lm()) is fitted and analysed in detail, including residual diagnostics, formal tests, and the plotting of fitted values with confidence bands. Note that only one predictor variable is allowed, as the function is designed for two-dimensional visualisation.

Both variables categorical: Comparing proportions

When both variables are categorical, no direction is assumed; the order of variables in the function call does not affect the test statistic, but it does influence the graphical output. For consistency, we continue referring to the variables as predictor and response.

visstat() tests the null hypothesis that the variables are independent using either Pearson’s $\chi^2$ test (chisq.test()) or Fisher’s exact test (fisher.test()), depending on expected cell counts. The choice of test is based on Cochran’s rule (Cochran 1954), which advises that the $\chi^2$ approximation is reliable only if no expected cell count is less than 1 and no more than 20 percent of cells have expected counts below 5.

Numeric response and categorical predictor: Comparing central tendencies

When the predictor consists of class “factor” with two or more levels and the response is of class “numeric” or “integer” (both having mode “numeric”), statistical tests are applied to compare the central tendencies across groups. This section describes the conditions under which parametric and non-parametric tests are chosen, based on the response type, the number of factor levels, and the underlying distributional assumptions.

Categorical predictor with two levels: Welch’s t-test and Wilcoxon rank-sum

When the predictor variable has exactly two levels, Welch’s t-test or the Wilcoxon rank-sum test is applied.

Welch’s t-test (t.test())

Welch’s t-test (t.test()) assumes that the observations are independent and that the response variable is approximately normally distributed within each group.

It evaluates the null hypothesis that the means of two groups are equal without assuming equal variances.

The test statistic is given by (Welch 1947; Satterthwaite 1946)

$$t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}},$$ where $\bar{x}_1$ and $\bar{x}_2$ are the sample means, $s_1^2$ and $s_2^2$ the sample variances, and $n_1$, $n_2$ the sample sizes in the two groups. The statistic follows a t-distribution with degrees of freedom approximated by the Welch-Satterthwaite equation:

$$\nu \approx \frac{ \left( \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} \right)^2 }{ \frac{(s_1^2 / n_1)^2}{n_1 - 1} + \frac{(s_2^2 / n_2)^2}{n_2 - 1} }.$$

The resulting p-value is computed from the t-distribution with $\nu$ degrees of freedom.

Welch’s t-test remains valid and exhibits only minimal loss of power even when the assumptions of Student’s t-test – namely, normality and equal variances of the response variable across groups – are satisfied (Moser and Stevens 1992; Delacre, Lakens, and Leys 2017). It is therefore the default implementation of the t-test in R.

Wilcoxon rank-sum test (wilcox.test())

The two-sample Wilcoxon rank-sum test (also known as the Mann-Whitney test) is a non-parametric alternative that does not require the response variable to be approximately normally distributed within each group. It tests for a difference in location between two independent distributions (Mann and Whitney 1947). If the two groups have distributions that are sufficiently similar in shape and scale, the Wilcoxon rank-sum test can be interpreted as testing whether the medians of the two populations are equal (Hollander, Chicken, and Wolfe 2014).

The two-level factor variable x defines two groups, with sample sizes $n_1$ and $n_2$. All $N=n_1 + n_2$ observations are pooled and assigned ranks from $1$ to $N$. Let $W_1$ denote the sum of the ranks assigned to the group $x_1$ corresponding to the first level of x containing $n_1$ observations:

$$W_{1}= \sum_{i=1}^{n_1} R(x_{1,i})$$,

where $R(x_{1,i})$ is the rank of observation $x_{1,i}$ in the pooled sample.

The test statistic $W$ returned by wilcox.test() is then computed as

$$W =U_{1}=W_{1} - \frac{n_1(n_1 + 1)}{2}.$$ It corresponds to the Mann-Whitney (Mann and Whitney 1947) $U$ statistic of the first group.

If both groups contain fewer than 50 observations and the data contain no ties, the p-value is computed exactly. Otherwise, a normal approximation with continuity correction is used.

Graphical output

Both tests show two plot panes, the first for checking the assumption of normality in both groups, the second the actual data with the chosen test.

Welch’s t-test does not fit a regression model, so there are no “residuals” in the regression sense. Therefore the function vis_ttest_assumptions()generates histograms overlaid with the normal distribution for both groups acompanied by the p-values of shapiro.test() and ad.tset().

The graphical output of the second pane consists of box plots overlaid with jittered points to display individual observations. When Welch’s t-test is applied, the function includes confidence intervals based on the user-specified conf.level.

The function returns a list containing the results of the applied test and the summary statistics used to construct the plot.

Examples

Welch’s t-test

The Motor Trend Car Road Tests dataset (mtcars) contains 32 observations, where mpg denotes miles per (US) gallon, and am represents the transmission type (0 = automatic, 1 = manual).

mtcars$am <- as.factor(mtcars$am)
t_test_statistics <- visstat(mtcars$am, mtcars$mpg)

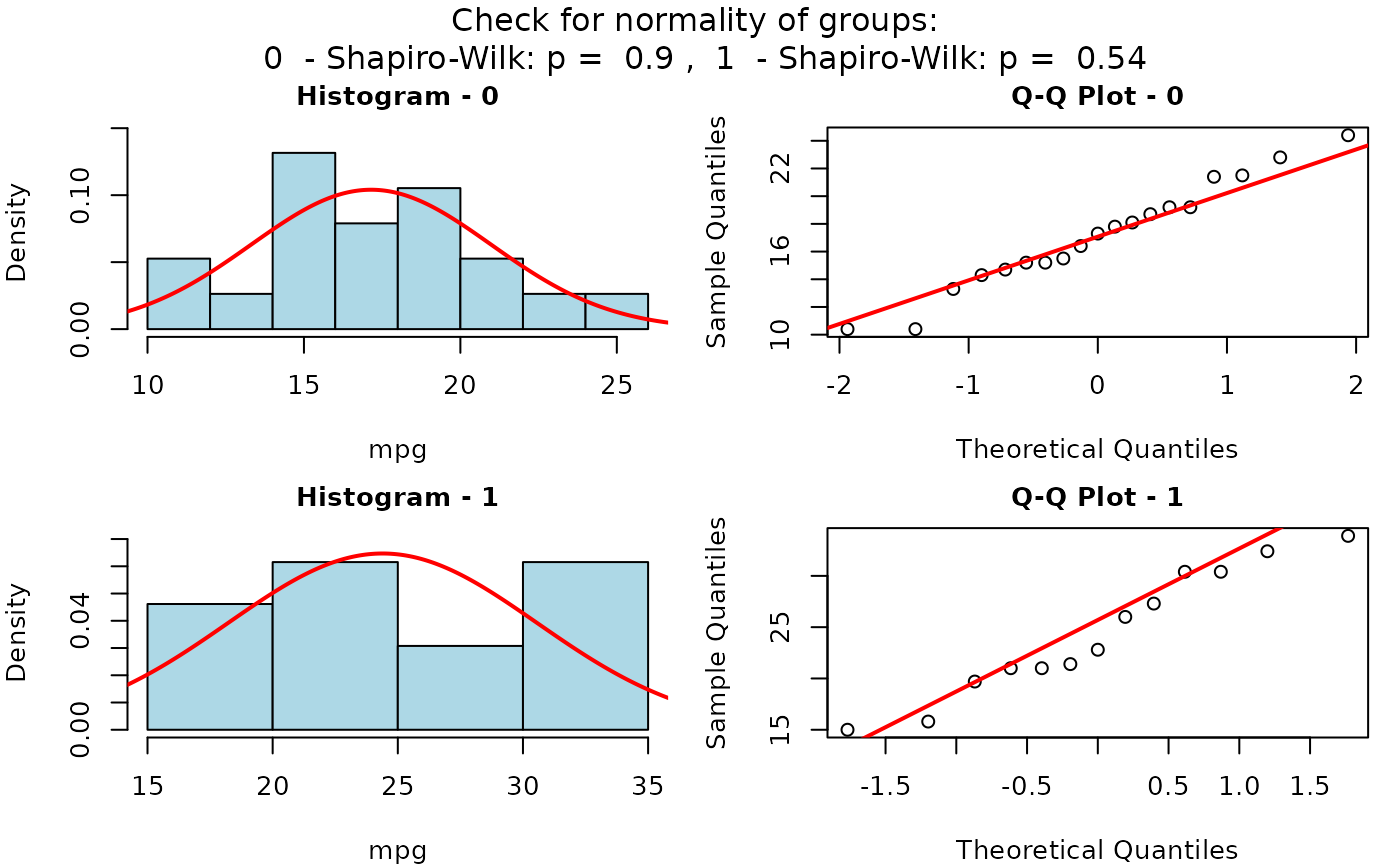
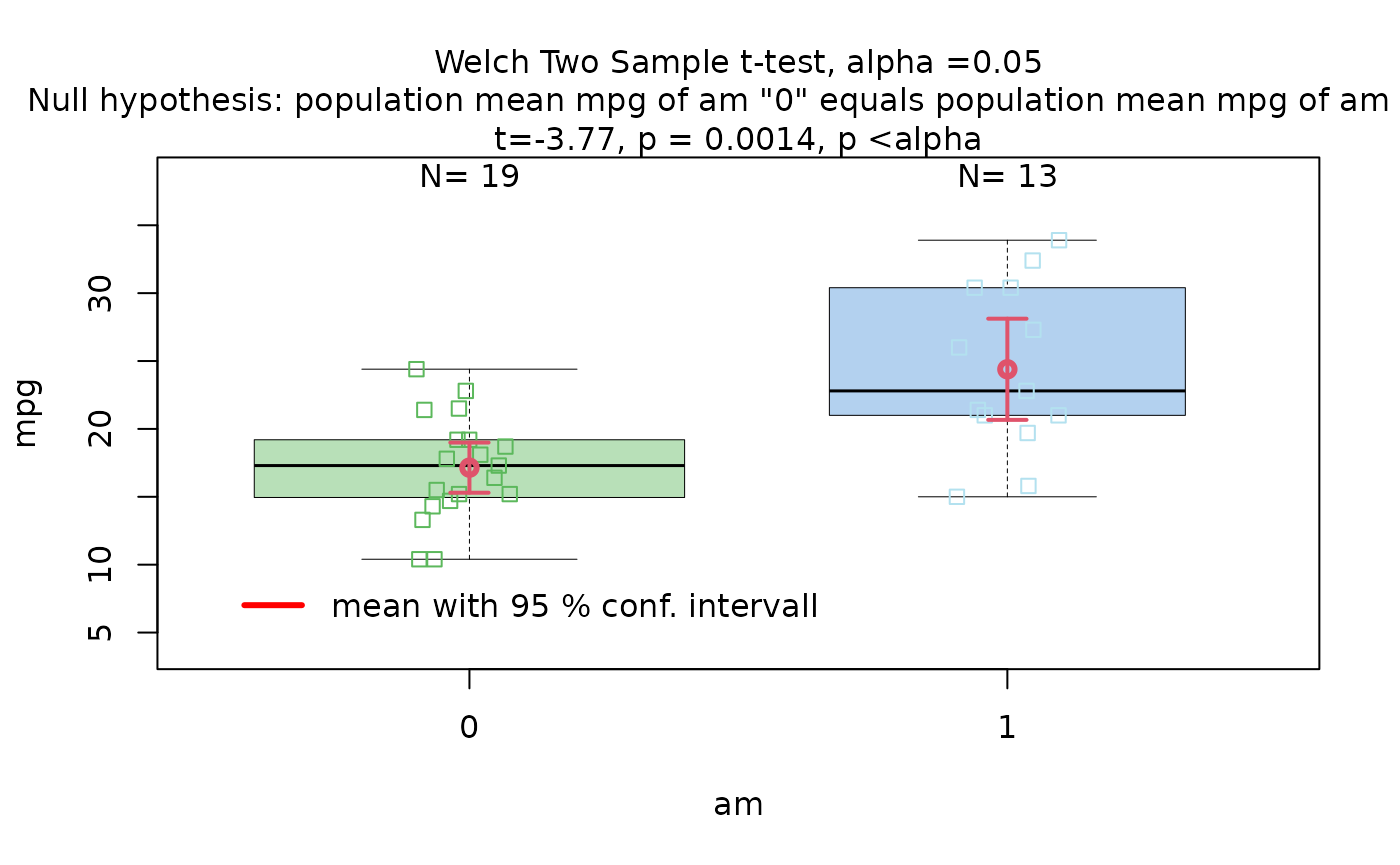
Increasing the confidence level conf.level from the default 0.95 to 0.99 results in wider confidence intervals, as a higher confidence level requires more conservative bounds to ensure that the interval includes the true parameter value with greater certainty.

Wilcoxon rank sum test

The Wilcoxon rank sum test is exemplified on differences between the central tendencies of grades of “boys” and “girls” in a class:

grades_gender <- data.frame(
  sex = as.factor(c(rep("girl", 21), rep("boy", 23))),
  grade = c(
    19.3, 18.1, 15.2, 18.3, 7.9, 6.2, 19.4,
    20.3, 9.3, 11.3, 18.2, 17.5, 10.2, 20.1, 13.3, 17.2, 15.1, 16.2, 17.0,
    16.5, 5.1, 15.3, 17.1, 14.8, 15.4, 14.4, 7.5, 15.5, 6.0, 17.4,
    7.3, 14.3, 13.5, 8.0, 19.5, 13.4, 17.9, 17.7, 16.4, 15.6, 17.3, 19.9, 4.4, 2.1
  )
)

wilcoxon_statistics <- visstat(grades_gender$sex, grades_gender$grade)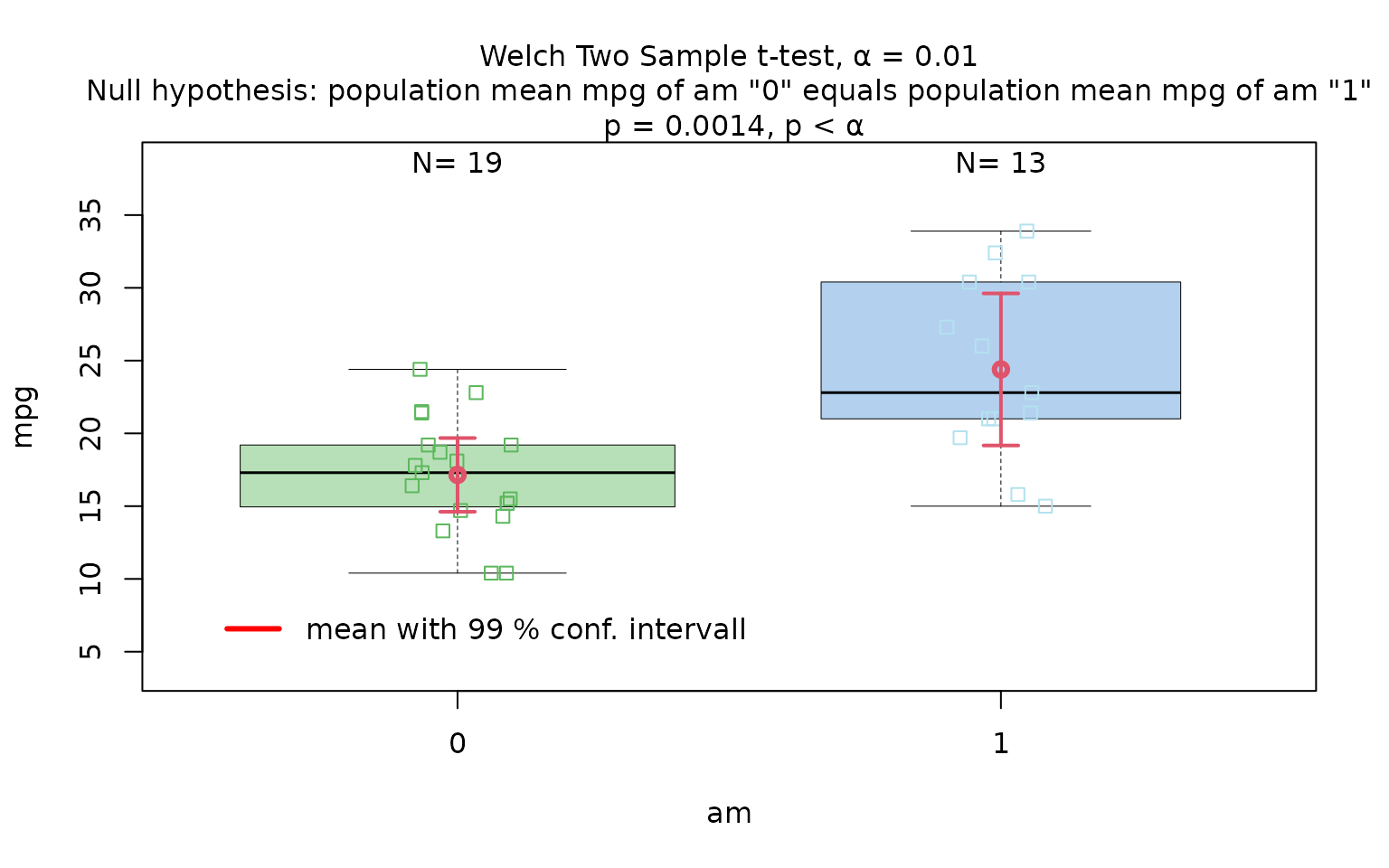

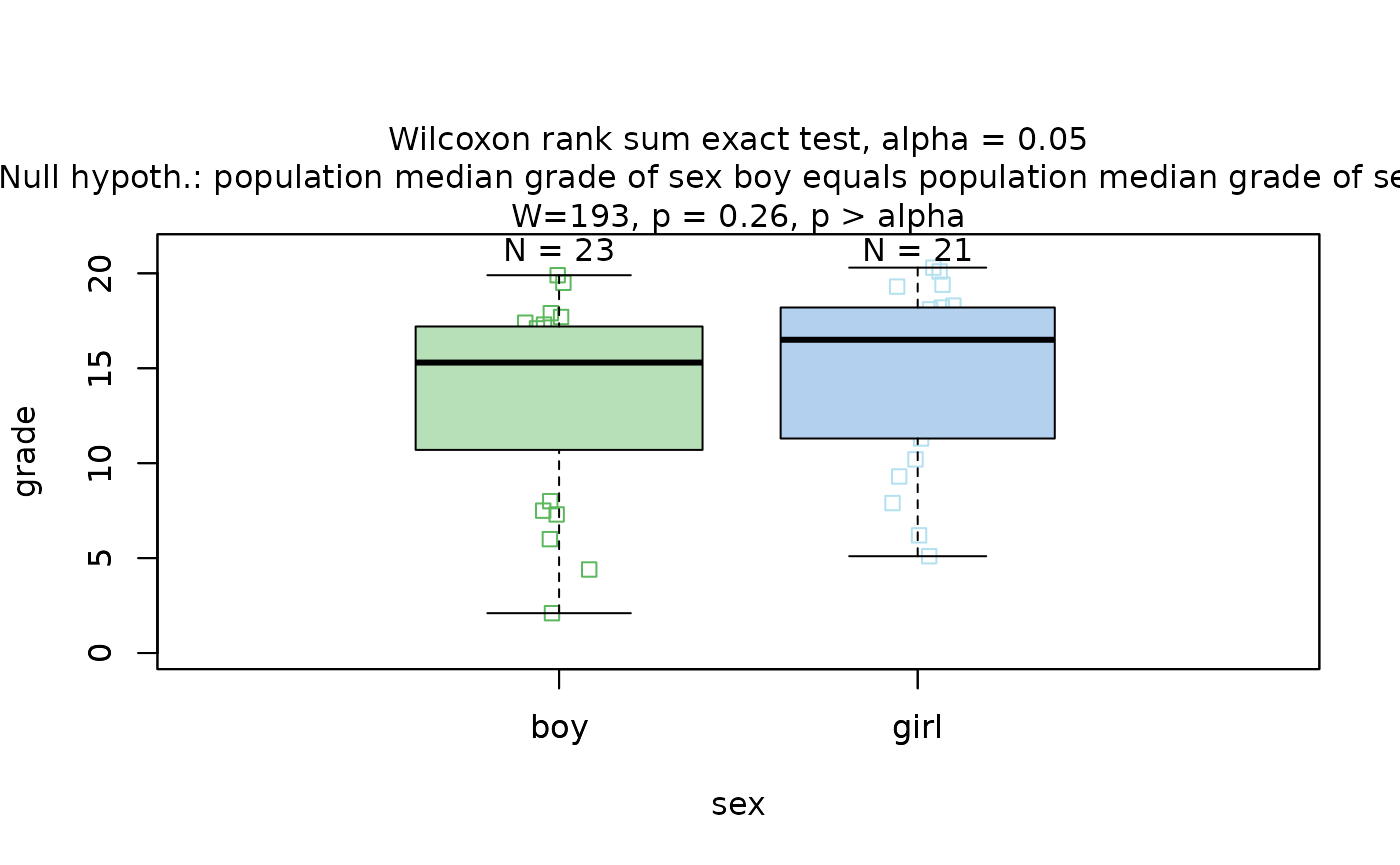
Categorical predictor with more than two levels

If the predictor is of class “factor” with more than two levels and the response is of mode “numeric”, visstat() either performs Fisher’s one- way ANOVA (Roland A. Fisher 1971) (aov()), Welch’s heteroscedastic one-way ANOVA (Welch 1951) (oneway.test()) or, as a non-parametric alternative, the Kruskal -Wallis test (Kruskal and Wallis 1952) (kruskal.test()).

In the remainder of this section, we briefly introduce the tests themselves, the assumption checks, and the post-hoc procedures, and illustrate each test with an example.

Fisher’s one-way ANOVA (aov())

Fisher’s one-way ANOVA (aov()) tests the null hypothesis that the means of multiple groups are equal. It assumes independent observations, normally distributed residuals, and homogeneous variances across groups. The test statistic is the ratio of the variance explained by differences among group means (between-group variance) to the unexplained variance within groups (Ronald A. Fisher and Yates 1990)

$$F = \frac{MS_{between}}{MS_{within}}= \frac{SS_{between}/(k-1)}{SS_{within}/(N-k)}== \frac{\frac{\sum_{i=1}^{k} n_i (\bar{x}_i - \bar{x})^2}{k - 1}} {\frac{\sum_{i=1}^{k}\sum_{j=1}^{n_i}(x_{ij}-\bar{x}_i)^2}{N - k}}$$

where: - where $MS_{between}$ and $MS_{within}$ are the mean square between groups and mean Square within groups respectively. - $SS_{between}$ = Sum of Squares between groups (variance due to group differences) - $SS_{within}$ = Sum of Squares within groups (error variance)
- $k$ = number of groups - $N$ = total sample size

where $\bar{x}_i$ is the mean of group $i$, $\bar{x}$ is the overall mean, $x_{ij}$ is the observation $j$ in group $i$, $n_i$ is the sample size in group $i$, $k$ is the number of groups, and $N$ is the total number of observations.

Under the null hypothesis, this statistic follows an F-distribution with two parameters for degrees of freedom: ($k - 1$) and ($N - k$): $F \sim F(k-1, N-k)$ The resulting p-value is computed from this distribution.

Welch’s heteroscedastic one-way ANOVA (oneway.test())

When only the assumptions of independent observations and normally distributed residuals are met, but homogeneous variances across groups cannot be assumed , Welch’s heteroscedastic one-way ANOVA (oneway.test()) (Welch 1951) provides an alternative to aov(). It compares group means using weights based on sample sizes and variances. The degrees of freedom are adjusted using a Satterthwaite-type approximation (Satterthwaite 1946), resulting in an F-statistic with non-integer degrees of freedom.

Kruskal–Wallis test (kruskal.test())

When the assumption of normality is not met, the Kruskal–Wallis test provides a non-parametric alternative. It compares group distributions based on ranked values and tests the null hypothesis that the groups come from the same population — specifically, that the distributions have the same location (Kruskal and Wallis 1952). If the group distributions are sufficiently similar in shape and scale, then the Kruskal–Wallis test can be interpreted as testing for equality of medians across groups (Hollander, Chicken, and Wolfe 2014).

The test statistic is defined as:

$$H = \frac{12}{N(N+1)} \sum_{i=1}^{k} n_i \left(\bar{R}_i - \bar{R} \right)^2,$$

where $n_i$ is the sample size in group $i$, $k$ is the number of groups, $\bar{R}_i$ is the average rank of group $i$, $N$ is the total sample size, and $\bar{R} = \frac{N+1}{2}$ is the average of all ranks. Under the null hypothesis, $H$ approximately follows a $\chi^2$ distribution with $k - 1$ degrees of freedom.

Testing the assumptions (vis_anova_assumptions())

The test logic for aov() and oneway.test() follows from their respective assumptions. visstat() initially models the data using aov() and analyses the residuals.

If both of the following conditions are met: (1) the standardised residuals follow the standard normal distribution, and (2) the residuals exhibit homoscedasticity (equal variances across groups), then the test statistic from aov() is returned.

If only the normality assumption is satisfied, visstat() applies oneway.test(). If the normality assumption is violated, kruskal.test() is used instead.

These assumptions are tested using the vis_anova_assumptions() function.

Controlling the family-wise error rate

ANOVA is an omnibus test that evaluates a single null hypothesis: all group means are equal. If the null hypothesis gets rejected, we would like to identify which specific groups differ significantly from each other. However, simple pairwise comparisons of group means following an ANOVA increases the probability of incorrectly declaring a significant difference when, in fact, there is none.

This error is quantified by the family-wise error rate “alpha per family of tests” $\alpha_{PF}$, which refers to the probability of making at least one Type I error, that is, falsely rejecting the null hypothesis across all pairwise comparisons.

Given $n$ levels of the categorical variable, there are

$$M = \frac{n \cdot (n - 1)}{2}$$

pairwise comparisons possible, defining a family of tests (Abdi 2007). $M$ corresponds to the number of null hypotheses in the post hoc tests, each testing whether the means of two specific groups are equal.

Post-hoc analysis

Šidák correction

If $\alpha_{PT}$ (“alpha per test”) is the probability of making a Type I error in one comparison, then $1 - \alpha_{PT}$ is the probability of not making a Type I error in one comparison.

If all $M$ comparisons are independent of each other, the probability of making no Type I error across the entire family of pairwise comparisons is $(1 - \alpha_{PT})^M$. The family-wise error rate is then given by its complement (Abdi 2007):

$$\alpha_{PF} = 1 - (1 - \alpha_{PT})^M.$$

Solving the last equation defining $\alpha_{PF}$ for $\alpha_{PT}$ yields the Šidák equation (Šidák 1967):

$$\alpha_{PT}=1-(1-{\alpha_{PF}})^{1/M}.$$ This shows that, in order to achieve a given family-wise error rate, the corresponding per-test significance level must be reduced when there are more than two groups.

visstat() sets $\alpha_{PF}$ to the user-defined $\alpha = 1 -$conf.level, resulting in

$$\alpha_{PT} = 1 - \texttt{conf.level}^{1 / M}.$$

With the default setting conf.level = 0.95, this leads to:

• $n = 3$ groups: $\alpha_{PT} = 1.70\%$
• $n = 6$ groups: $\alpha_{PT} = 0.34\%$
• $n = 10$ groups: $\alpha_{PT} = 0.11\%$

These examples illustrate that the Šidák approach becomes increasingly conservative as the number of comparisons grows. Moreover, since the method assumes independence among tests, it may be overly conservative when this assumption is violated.

Post-hoc test following an ANOVA: TukeyHSD()

In contrast to the general-purpose Šidák correction, Tukey’s Honestly Significant Differences procedure (TukeyHSD()) is specifically designed for pairwise mean comparisons following an ANOVA (either aov() or oneway.test()). It controls the family-wise error rate using a critical value from the studentised range distribution, which properly accounts for the correlated nature of pairwise comparisons sharing a common residual variance (Hochberg and Tamhane 1987).

Based on the user-specified confidence level (conf.level), visstat() constructs confidence intervals for all pairwise differences between factor level means. A significant difference between two means is indicated when the corresponding confidence interval does not include zero. visstat() returns both the HSD-adjusted p-values and the associated confidence intervals for all pairwise comparisons.

For graphical display, visstat() uses a dual approach: TukeyHSD() provides the statistical test results and significance determinations, while Šidák-corrected confidence intervals around individual group means are shown for visualisation purposes. This separation allows for optimal statistical testing while maintaining clear, interpretable graphics.

Post-hoc test following the Kruskal–Wallis rank sum test: pairwise.wilcox.test()

As a post-hoc analysis following the Kruskal–Wallis test, visstat() applies the pairwise Wilcoxon rank sum test using pairwise.wilcox.test() to compare each pair of factor levels (see section “Wilcoxon rank-sum test (wilcox.test())”).

The resulting p-values from all pairwise comparisons are then adjusted for multiple testing using Holm’s method (Holm 1979): The p-values are first sorted from smallest to largest and tested against thresholds that become less strict as their rank increases. This stepwise adjustment does not assume independence among tests and is typically less conservative than the Šidák method, while still ensuring strong control of the family-wise error rate.

Graphical output

The graphical output for all tests based on a numeric response and a categorical predictor with more than two levels consists of two panels: the first focuses on the residual analysis, the second on the actual test chosen by the decision logic.

The residual panel addresses the assumption of normality, both graphically and through formal tests. It displays a scatter plot of the standardised residuals versus the predicted values, as well as a normal Q–Q plot comparing the sample quantiles to the theoretical quantiles. If the residuals are normally distributed, no more than $5\%$ of the standardised residuals should exceed approximately $|2|$; in the Q–Q plot the data points should approximately follow the red straight line.

The p-values of the formal tests for normality (Shapiro–Wilk and Anderson–Darling) as well as the tests for homoscedasticity (Bartlett’s and Levene Brown–Forsythe) are given in the title.

visstat() then illustrates, in the subsequent graph, either the kruskal.test(), the oneway.test(), or aov() result (see also Section “Decision logic”).

If neither normality of the residuals nor homogeneity of variances is given, the kruskal.test() is executed. The result is illustrated using box plots alongside jittered data points, with the title displaying the p-value from kruskal.test().

Above each box plot, the number of observations per level is shown. Different green letters below a pair of box plots indicate that the two groups are considered significantly different based on Holm’s-adjusted pairwise Wilcoxon rank sum test p-values smaller than $\alpha$. The letters are generated with the help of the function multcompLetters() from the multcompView package (Graves, Piepho, and with help from Sundar Dorai-Raj 2024)).

If normality of the residuals can be assumed, a parametric test is chosen: either aov(), if homoscedasticity is also assumed, or oneway.test() otherwise. visstat() displays the name of the test and the corresponding $F$ and p-value in the title.

The graph shows both the conf.level $\cdot\,100\%$ confidence intervals corresponding to the null hypothesis of ANOVA (all group means are equal) and the Šidák-corrected $(1 - \alpha_{PT}) \cdot 100\%$ confidence intervals used in the post hoc analysis.

In visstat(), the Šidák intervals are used only for visualisation, as the underlying method assumes independent comparisons and can become overly conservative when this assumption is violated.

The actual post hoc analysis should be based on TukeyHSD(). A significant test result between two groups is graphically represented by different green letters below a pair of group means.

Besides the graphical output, visstat() returns a list containing the relevant test statistics along with the corresponding post-hoc-adjusted $p$-values for all pairwise comparisons.

Examples

ANOVA

The npk dataset reports the yield of peas (in pounds per block) from an agricultural experiment conducted on six blocks. In this experiment, the application of three different fertilisers – nitrogen (N), phosphate (P), and potassium (K) – was varied systematically. Each block received either none, one, two, or all three of the fertilisers,

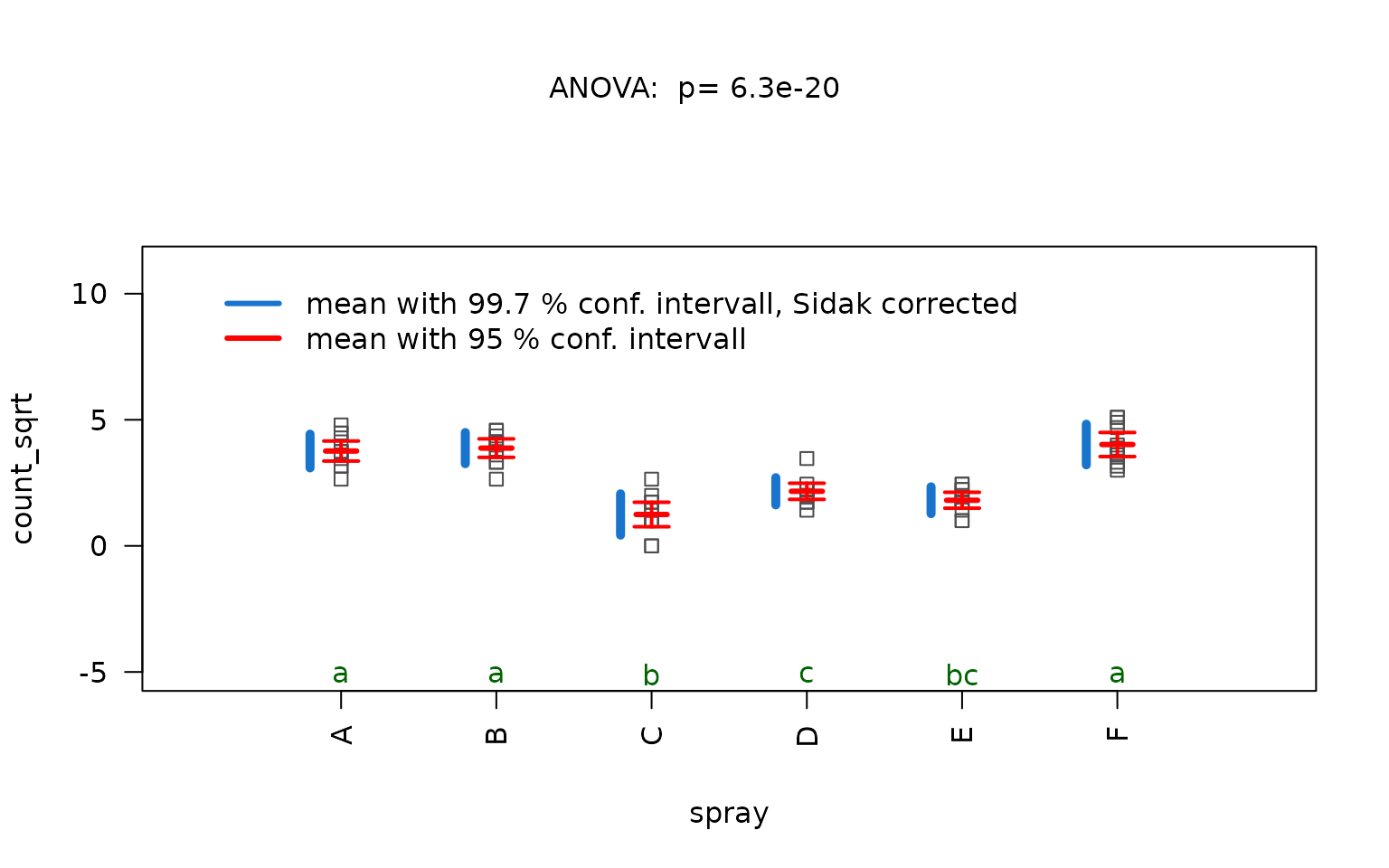
anova_npk <- visstat(npk$block,npk$yield,conf.level=0.90)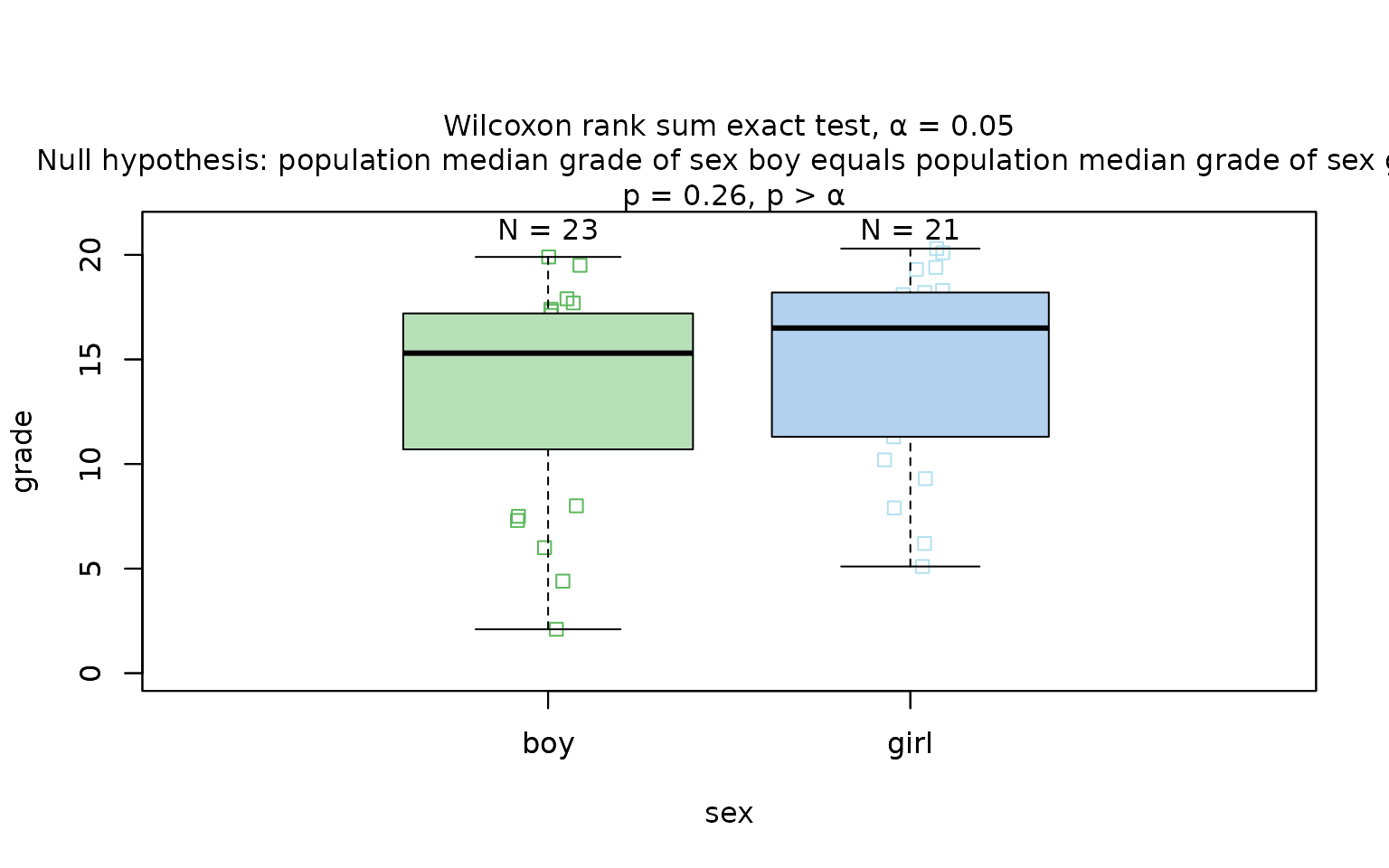

Normality of residuals is supported by graphical diagnostics (histogram, scatter plot of standardised residuals, Q-Q plot) and formal tests (Shapiro–Wilk and Anderson- Darling, both with $p > \alpha$).homogeneity of variances is not supported at the given confidence level by bartlett.test(), but by levene.test() ($p > \alpha$). The decision logic is based on levene.test() and triggers aov(). Post-hoc analysis with TukeyHSD() shows no significant yield differences between blocks, as all share the same group label (e.g., all green letters).

Kruskal–Wallis rank sum test

The iris dataset contains petal width measurements (in cm) for three different iris species.

visstat(iris$Species, iris$Petal.Width)

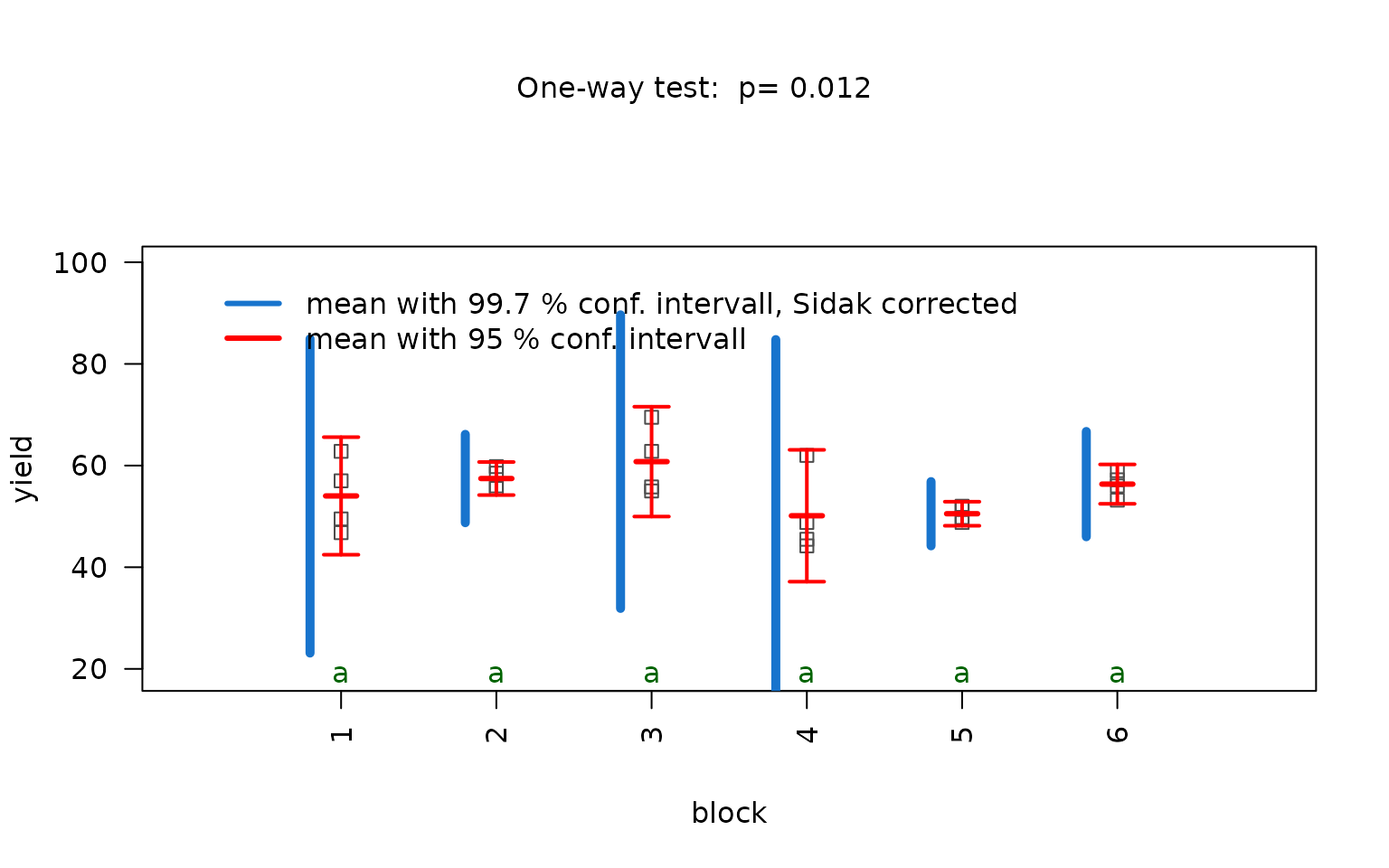
In this example, scatter plots of the standardised residuals and the Q-Q plot suggest that the residuals are not normally distributed. This is confirmed by very small p-values from both the Shapiro–Wilk and Anderson-Darling tests.

If both p-values are below the significance level $\alpha$, visstat() switches to the non-parametric kruskal.test(). Post-hoc analysis using pairwise.wilcox.test() shows significant differences in petal width between all three species, as indicated by distinct group labels (all green letters differ).

Numeric response and numeric predictor: Simple linear regression

Simple linear regression (lm())

If both the predictor and the response are numeric and contain only one level each, visstat() performs a simple linear regression.

The resulting regression plot displays the point estimate of the regression line

$$y = a + b \cdot x,$$

where $y$ is the response variable, $x$ is the predictor variable, $a$ is the intercept, and $b$ is the slope of the regression line.

Residual analysis

visstat() checks the normality of the standardised residuals from lm() both with diagnostic plots and using the Shapiro–Wilk and Anderson-Darling tests. (via visAnovassumptions())

Note, that regardless of the result of the residual analysis, visstat() proceeds to perform the regression. The title of the graphical output indicates the chosen confidence level (conf.level), the estimated regression parameters with their confidence intervals and p-values, and the adjusted $R^2$. The plot displays the raw data, the fitted regression line, and both the confidence and prediction bands corresponding to the specified conf.level.

visstat() returns a list containing the regression test statistics, the p-values from the normality tests of the standardised residuals, and the pointwise estimates of the confidence and prediction bands.

Examples

dataset: `trees``

The trees data set contains the diameter Girth in inches and Volume in cubic ft of 31 black cherry trees.

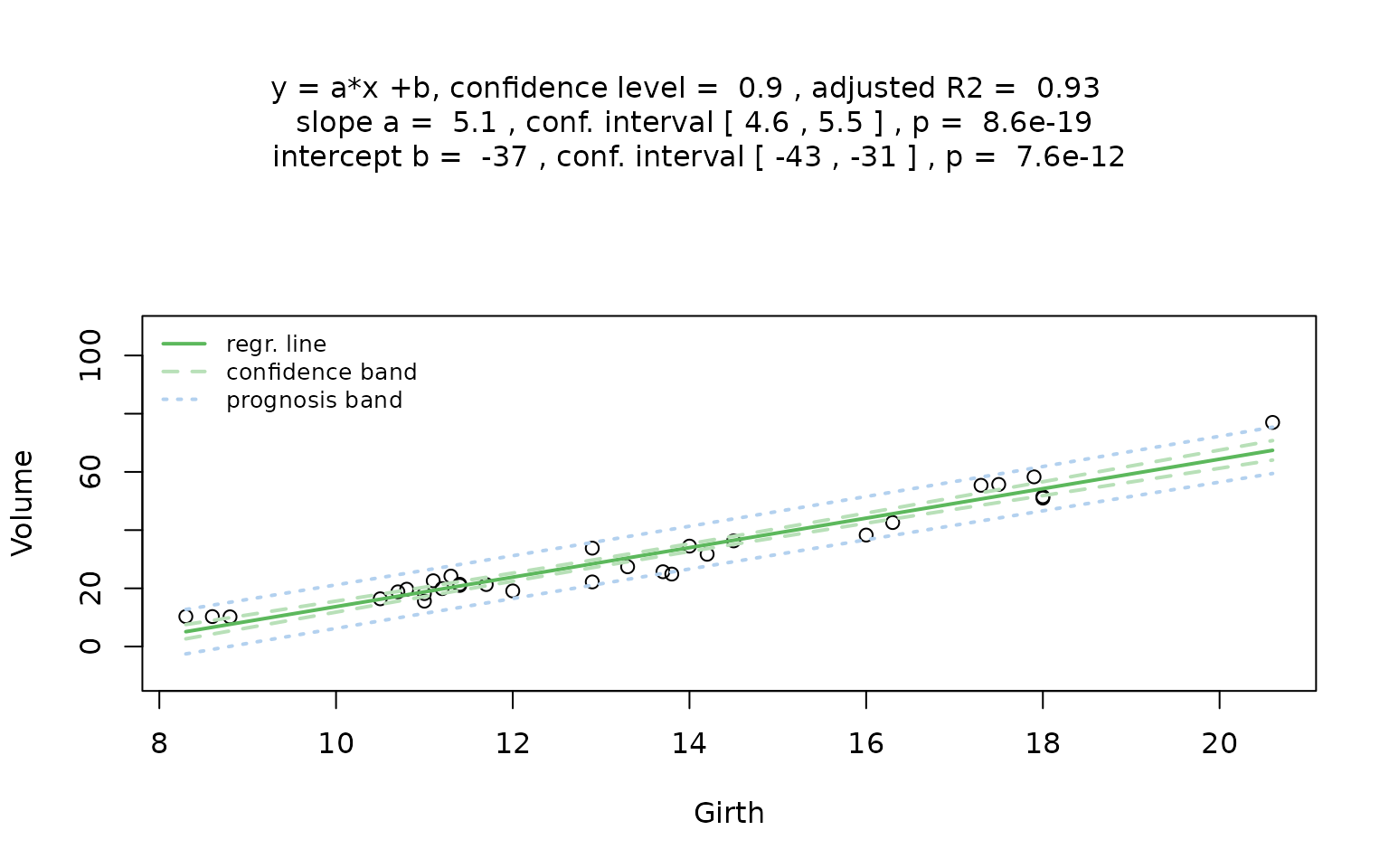
linreg_trees <- visstat(trees$Girth, trees$Volume,conf.level=0.9)

p-values greater than conf.level in both the Anderson-Darling normality test and the Shapiro–Wilk test of the standardised residuals indicate that the normality assumption of the residuals underlying the linear regression is met.

Increasing the confidence level conf.level from the default 0.9 to 0.99 results in wider confidence intervals of the regression parameters as well as wider confidence and prediction bands

linreg_trees_99 <- visstat(trees$Girth, trees$Volume,conf.level = 0.99)

The visStatistics plot allows to display only the second generated plot (the assumption plot is unchanged):

plot(linreg_trees_99,which=2)

Both variables categorical: Comparing proportions

When both variables are categorical (i.e., of class factor), visstat() tests the null hypothesis that the two variables are independent. Observed frequencies are typically arranged in a contingency table, where rows index the levels $i$ of the response variable and columns index the levels $j$ of the predictor variable.

Pearson’s residuals and mosaic plots

Mosaic plots provide a graphical representation of contingency tables, where the area of each tile is proportional to the observed cell frequency. To aid interpretation, tiles are coloured based on Pearson residuals from a chi-squared test of independence. These residuals measure the standardised deviation of observed from expected counts under the null hypothesis of independence.

Let $O_{ij}$ and $E_{ij}$ denote the observed and expected frequencies in row $i$ and column $j$ of an $R \times C$ contingency table. The Pearson residual for each cell is defined as

$$r_{ij} = \frac{O_{ij} - E_{ij}}{\sqrt{E_{ij}}}, \quad i = 1, \ldots, R,\quad j = 1, \ldots, C.$$ Positive residuals (shaded in blue) indicate observed counts greater than expected, while negative values suggest under-representation (shaded in red). Colour shading thus highlights which combinations of categorical levels contribute most to the overall association.

Pearson’s $\chi^2$-test (chisq.test())

The test statistic of Pearson’s $\chi^2$-test (Pearson 1900) is the sum of squared Pearson residuals:

$$\chi^2 = \sum_{i=1}^{R} \sum_{j=1}^{C} r_{ij}^2 = \sum_{i=1}^{R} \sum_{j=1}^{C} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}.$$

The test statistic is compared to the chi-squared distribution with $ (R - 1)(C - 1)$ degrees of freedom. The resulting p-value corresponds to the upper tail probability — that is, the probability of observing a value greater than or equal to the test statistic under the null hypothesis.

Pearson’s $\chi^2$ test with Yates’ continuity correction

Yates’ correction is applied to the Pearson $\chi^2$ statistic in $2 \times 2$ contingency tables (with one degree of freedom). In this case, the approximation of the discrete sampling distribution by the continuous $\chi^2$ distribution tends to overestimate the significance level of the test. To correct for this, Yates proposed subtracting 0.5 from each absolute difference between observed and expected counts (Yates 1934), resulting in a smaller test statistic: $$\chi^2_{\text{Yates}} = \sum_{i=1}^{2} \sum_{j=1}^{2} \frac{(|O_{ij} - E_{ij}| - 0.5)^2}{E_{ij}}.$$

This reduced test statistic yields a larger p-value, thereby lowering the risk of a Type I error.

Yates’ continuity correction is applied by default by the underlying routine chisq.test(). ## Fisher’s exact test (fisher.test())

The $\chi^2$ approximation is considered reliable only if no expected cell count is less than 1 and no more than 20 percent of cells have expected counts below 5 (Cochran 1954)). If this condition is not met, Fisher’s exact test (Ronald Aylmer Fisher 1970) (fisher.test()) is applied instead, as it is a non-parametric method that does not rely on large-sample approximations. The test calculates an exact p-value for testing independence by conditioning on the observed margins: the row totals $R_i = \sum_{j=1}^C O_{ij}$ and the column totals $C_j = \sum_{i=1}^R O_{ij}$, defining the structure of the contingency table.

In the $2 \times 2$ case, the observed table can be written as:

$$\begin{array}{c|cc|c} & C_1 & C_2 & \text{Row sums} \\\\ \hline R_1 & a & b & a + b \\\\ R_2 & c & d & c + d \\\\ \hline \text{Column sums} & a + c & b + d & n \end{array}$$

Let $$O = \begin{bmatrix} a & b \\\\ c & d \end{bmatrix}$$ denote the above observed $2 \times 2$ contingency table. The exact probability of observing this table under the null hypothesis of independence, given the fixed margins, is given by the hypergeometric probability mass function (PMF)

$$\mathbb{P}(O \mid R_1, R_2, C_1, C_2) = \frac{\binom{a + b}{a} \binom{c + d}{c}}{\binom{n}{a + c}},$$

where $n = a + b + c + d$ is the total sample size.

The p-value is computed by summing the probabilities of all tables with the same margins whose probabilities under the null are less than or equal to that of the observed table.

For general $R \times C$ tables, fisher.test() generalises this approach using the multivariate hypergeometric distribution.

Test choice and graphical output

If the expected frequencies are sufficiently large - specifically, if at least 80% of the cells have expected counts greater than 5 and no expected count is smaller than 1, the function uses Pearson’s ${\chi}^2$-test (chisq.test()).

Otherwise, it switches to Fisher’s exact test (fisher.test()) (Cochran 1954).

For 2-by-2 contingency tables, Yates’ continuity correction (Yates 1934) is always applied to Pearson’s ${\chi}^2$-test.

For all tests of independence visstat() displays a grouped column plot that includes the respective test’s p-value in the title, as well as a mosaic plot showing colour-coded Pearson residuals and the p-value of Pearson’s $\chi^2$-test.

Transforming a contingency table to a data frame

The following examples for tests of categorical predictor and response are all based on the HairEyeColor contingency table.

Contingency tables must be converted to the required column-based data.frame using the helper function counts_to_cases(). The function transforms the contingency table HairEyeColor into data.frame named HairEyeColourDataFrame.

HairEyeColourDataFrame <- counts_to_cases(as.data.frame(HairEyeColor))

Examples

In all examples of this section, we will test the null hypothesis that hair colour (“Hair”) and eye colour (“Eye”) are independent of each other.

Pearson’s ${\chi}^2$-test (chisq.test())

hair_eye_colour_df <- counts_to_cases(as.data.frame(HairEyeColor))
visstat(hair_eye_colour_df$Eye, hair_eye_colour_df$Hair)

The graphical output shows that the null hypothesis of Pearson’s $\chi^2$ test – namely, that hair colour and eye colour are independent – must be rejected at the default significance level $\alpha=0.05$ ($p = 2.33 \cdot 10^{-25} < \alpha$). The mosaic plot indicates that the strongest deviations are due to over-representation of individuals with black hair and brown eyes, and of those with blond hair and blue eyes. In contrast, individuals with blond hair and brown eyes are the most under-represented.

Pearson’s ${\chi}^2$-test with Yate’s continuity correction

In the following example, we restrict the data to participants with either black or brown hair and either brown or blue eyes, resulting in a 2-by-2 contingency table.

hair_black_brown_eyes_brown_blue <- HairEyeColor[1:2, 1:2, ]
# Transform to data frame
hair_black_brown_eyes_brown_blue_df <- counts_to_cases(as.data.frame(hair_black_brown_eyes_brown_blue))
# Chi-squared test
visstat(hair_black_brown_eyes_brown_blue_df$Eye, hair_black_brown_eyes_brown_blue_df$Hair)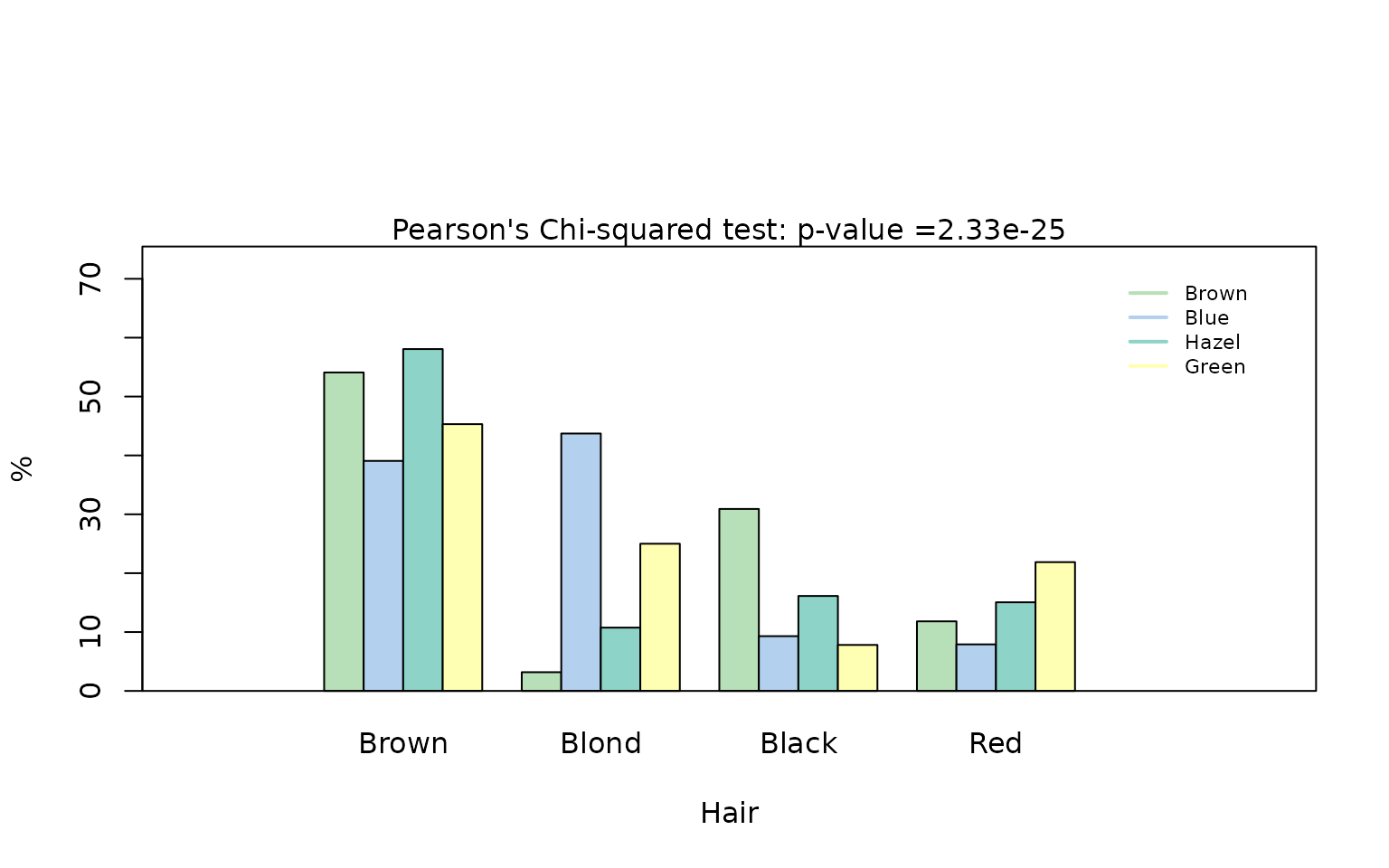

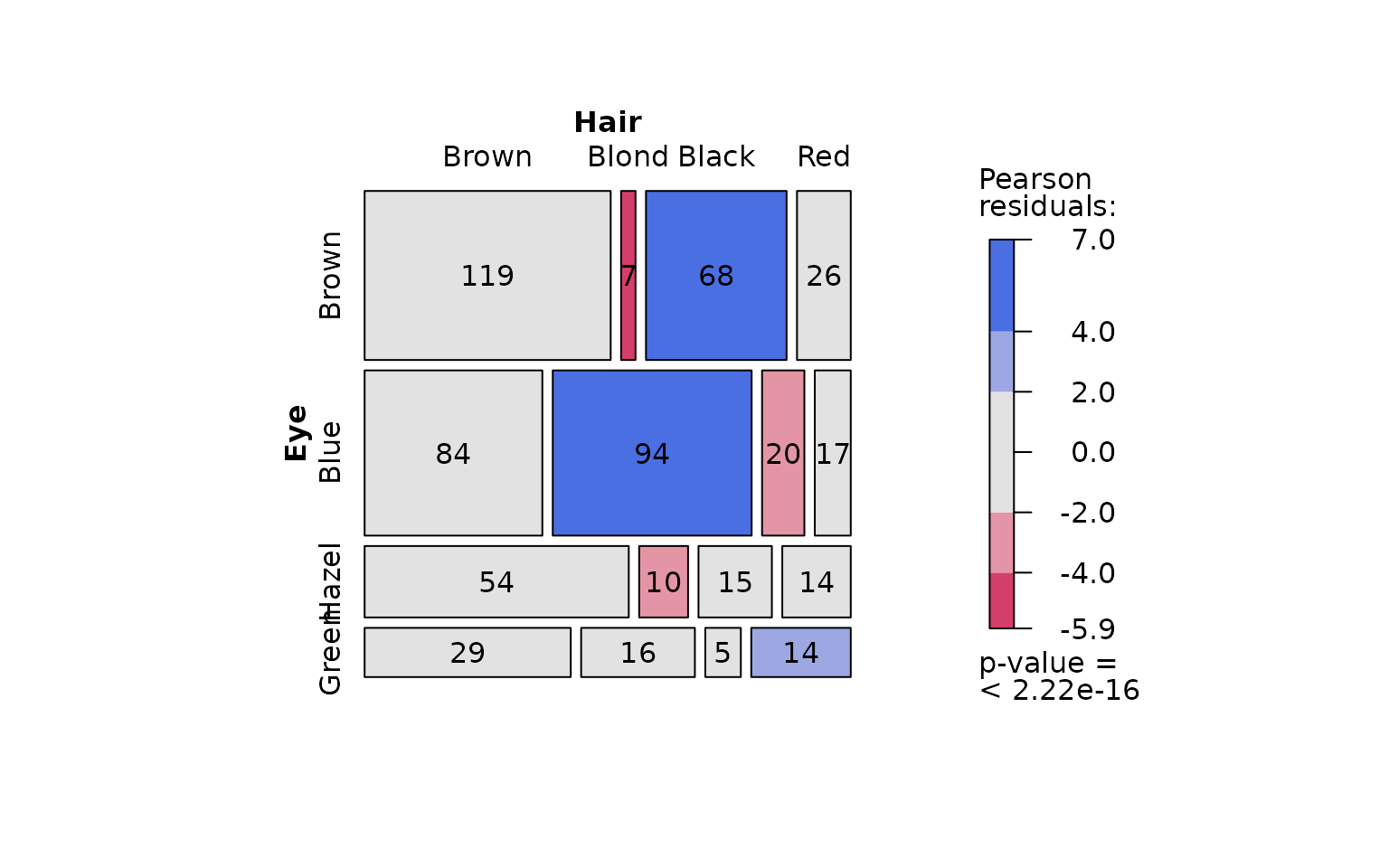
Also in this reduced dataset we reject the null hypothesis of independence of the hair colors “brown” and “black” from the eye colours “brown” and ” blue”. The mosaic plot shows that blue-eyed persons with black hair are under- represented. Note the higher p-value of Pearson’s ${\chi}^2$-test with Yate’s continuity correction (p = 0.00354) compared to the p-value of Pearson’s ${\chi}^2$-test (p = 0.00229) shown in the mosaic plot.

Fisher’s exact test (fisher.test())

Again, we extract a 2-by-2 contingency table from the full dataset, this time keeping only male participants with black or brown hair and hazel or green eyes.

Pearson’s ${\chi}^2$ test applied to this table would yield an expected frequency less than 5 in one of the four cells (25% of all cells), which violates the requirement that at least 80% of the expected frequencies must be 5 or greater (Cochran 1954).

Therefore, visstat() automatically selects Fisher’s exact test instead.

hair_eye_colour_male <- HairEyeColor[, , 1]
# Slice out a 2 by 2 contingency table
black_brown_hazel_green_male <- hair_eye_colour_male[1:2, 3:4]
# Transform to data frame
black_brown_hazel_green_male <- counts_to_cases(as.data.frame(black_brown_hazel_green_male))
# Fisher test
fisher_stats <- visstat(black_brown_hazel_green_male$Eye, black_brown_hazel_green_male$Hair)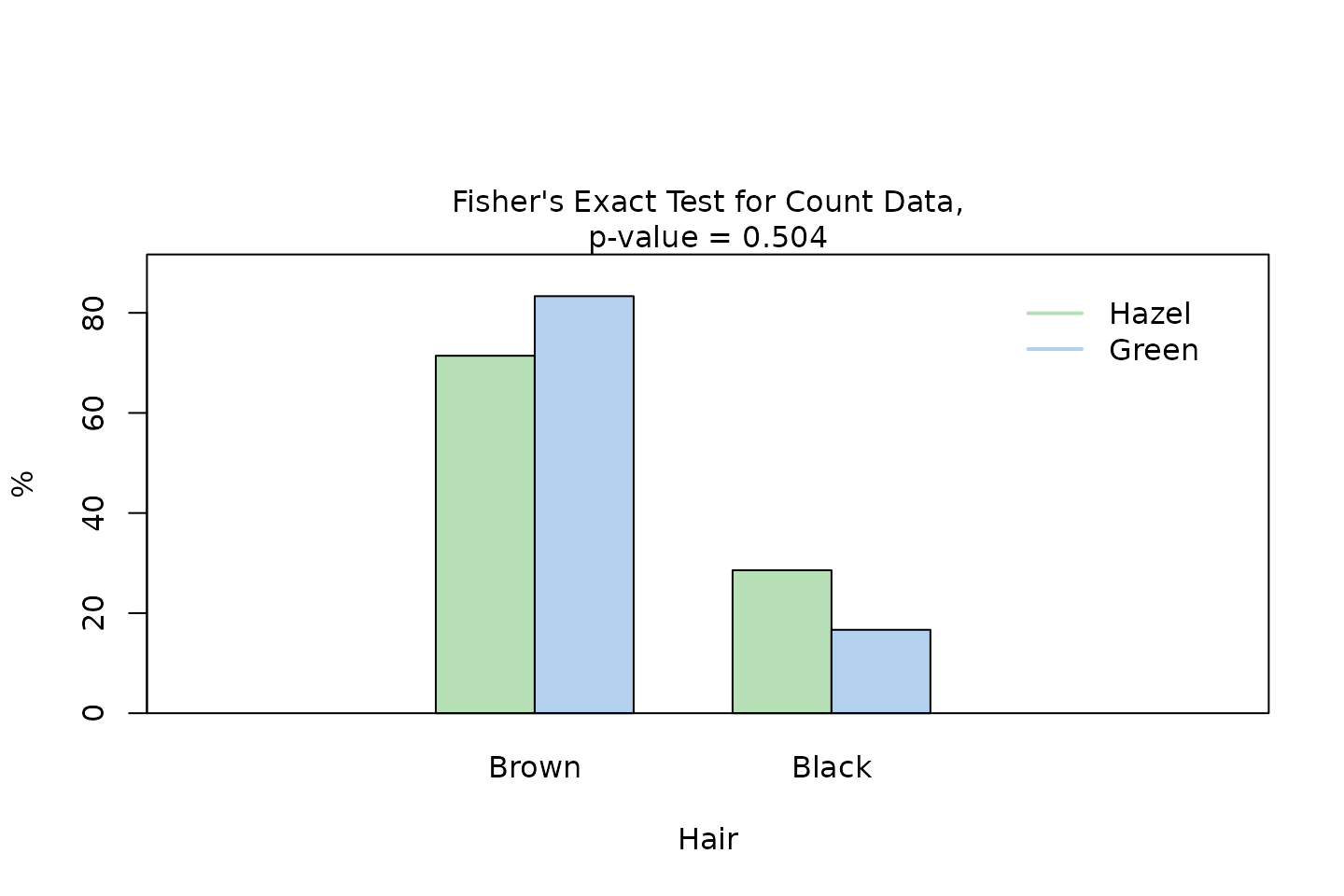

Saving the graphical output

All generated graphics can be saved in any file format supported by Cairo(), including “png”, “jpeg”, “pdf”, “svg”, “ps”, and “tiff” in the user specified plotDirectory.

If the optional argument plotName is not given, the naming of the output follows the pattern "testname_namey_namex.", where "testname" specifies the selected test and "namey" and "namex" are character strings naming the selected data vectors y and x, respectively. The suffix corresponding to the chosen graphicsoutput (e.g., "pdf", "png") is then concatenated to form the complete output file name.

In the following example, we store the graphics in png format in the plotDirectory tempdir() with the default naming convention:

#Graphical output written to plotDirectory: In this example 
# a bar chart to visualise the Chi-squared test and mosaic plot showing
# Pearson's residuals.
#chi_squared_or_fisher_Hair_Eye.png and mosaic_complete_Hair_Eye.png
save_fisher = visstat(black_brown_hazel_green_male, "Hair", "Eye",
        graphicsoutput = "png", plotDirectory = tempdir())

The full file path of the generated graphics are stored as the attribute "plot_paths" on the returned object of class "visstat".

paths <- attr(save_fisher, "plot_paths")
print(paths)

## [1] "/tmp/RtmpbBQmX3/chi_squared_or_fisher_Hair_Eye.png"
## [2] "/tmp/RtmpbBQmX3/mosaic_complete_Hair_Eye.png"

Remove the graphical output from plotDirectory:

file.remove(paths)

## [1] TRUE TRUE

When assumptions plots (residual and Q-Q plot) are generated, the corresponding plot has the prefix "assumption_.

Limitations

Limitations by default settings

The main purpose of this package is a decision-logic based automatic visualisation of statistical test results. Therefore, except for the user-adjustable conf.level parameter, all statistical tests are applied using their default settings from the corresponding base R functions. As a consequence, paired tests are currently not supported and visstat() does not allow to study interactions terms between the different levels of an independent variable in an analysis of variance. Focusing on the graphical representation of tests, only simple linear regression is implemented, as multiple linear regressions cannot be visualised.

Limitations of of decision-logic based on p-values

The decision logic of the main function visstat() is based on the Shapiro-Wilk test for normality and the Levene-Brown-Forsythe test for variance homogeneity. However, no single test maintains optimal Type I error rates and statistical power across all distributions (Olejnik and Algina 1987), and p-values obtained from these tests may be unreliable if their assumptions are violated.

Combining multiple tests with differing assumptions using simple majority voting inflates the overall Type I error rate, making such an approach inadequate. Therefore, automated test selection based solely on p-values cannot replace the visual inspection of sample distributions provided by visstat(). Based on the provided diagnostic plots, it may be necessary to override the automated choice of test in individual cases.

Bootstrapping as modern alternative to hypothesis testing

Bootstrapping methods (Wilcox 2021) make minimal distributional assumptions and can provide confidence intervals for nearly any statistic. However, bootstrapping is computationally intensive, often requiring thousands of resamples, and may perform poorly with very small sample sizes.

The computational intensity of bootstrap and runs counter to the purpose of the visStatistics package, which is designed to offer a rapid overview of the data, laying the groundwork for deeper analysis in subsequent steps.

The package targets users with basic statistical literacy, such as non-specialist professionals and students in applied fields. It covers topics typically included in an undergraduate course on applied statistics, intentionally excluding more advanced methods like bootstrapping to keep the focus on foundational concepts.

Implemented tests

Numeric response and categorical predictor

When the response is numeric and the predictor is categorical, a test of central tendency is selected:

t.test(), wilcox.test(), aov(), oneway.test(),kruskal.test()

Normality assumption check

shapiro.test() and ad.test() (Gross and Ligges 2015)

Homoscedasticity assumption check

bartlett.test() and levene.test()

Post-hoc tests

• TukeyHSD() (for aov()and oneway.test())
• pairwise.wilcox.test() (for kruskal.test())

Numeric response and numeric predictor

When both the response and predictor are numeric, a simple linear regression model is fitted:

lm()

Both variables categorical

When both variables are categorical, visstat() tests the null hypothesis of independence using one of the following:

• chisq.test() (default for larger samples)
• fisher.test() (used for small expected cell counts based on Cochran’s rule)

Bibliography

Abdi, Hervé. 2007. “The Bonferonni and Sidak Corrections for Multiple Comparisons.” Encyclopedia of Measurement and Statistics.

Allingham, David, and J. C. W. Rayner. 2012. “Testing Equality of Variances for Multiple Univariate Normal Populations.” Journal of Statistical Theory and Practice 6 (3): 524–35. https://doi.org/10.1080/15598608.2012.695703.

Bartlett, M. S. 1937. “Properties of Sufficiency and Statistical Tests.” Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 160 (901): 268–82. https://doi.org/10.1098/rspa.1937.0109.

Brown, Morton B., and Alan B. Forsythe. 1974. “Robust Tests for the Equality of Variances.” Journal of the American Statistical Association 69 (346): 364–67. https://doi.org/10.1080/01621459.1974.10482955.

Cochran, William G. 1954. “The Combination of Estimates from Different Experiments.” Biometrics 10 (1): 101. https://doi.org/10.2307/3001666.

Delacre, Marie, Daniël Lakens, and Christophe Leys. 2017. “Why Psychologists Should by Default Use Welch’s t-Test Instead of Student’s t-Test.” International Review of Social Psychology 30 (1): 92–101. https://doi.org/10.5334/irsp.82.

Fagerland, Morten W., and Leiv Sandvik. 2009. “Performance of Five Two-Sample Location Tests for Skewed Distributions with Unequal Variances.” Contemporary Clinical Trials 30 (5): 490–96. https://doi.org/10.1016/j.cct.2009.06.007.

Fisher, Roland A. 1971. The Design of Experiments. 9th ed. Macmillan.

Fisher, Ronald A., and F Yates. 1990. Statistical Methods, Experimental Design, and Scientific Inference: A Re-issue of Statistical Methods for Research Workers, the Design of Experiments and Statistical Methods and Scientific Inference. Edited by J H Bennett. Oxford University PressOxford. https://doi.org/10.1093/oso/9780198522294.001.0001.

Fisher, Ronald Aylmer. 1970. Statistical Methods for Research Workers. 14th ed., revised and enlarged. Edinburgh: Oliver and Boyd.

Fox, John, and Sanford Weisberg. 2019. An R Companion to Applied Regression. 3rd ed. Thousand Oaks CA: Sage.

Ghasemi, Asghar, and Saleh Zahediasl. 2012. “Normality Tests for Statistical Analysis: A Guide for Non-Statisticians.” Int J Endocrinol Metab 10 (2): 486–89. https://doi.org/10.5812/ijem.3505.

Graves, Spencer, Hans-Peter Piepho, and Luciano Selzer with help from Sundar Dorai-Raj. 2024. multcompView: Visualizations of Paired Comparisons. Manual. https://doi.org/10.32614/CRAN.package.multcompView.

Gross, Juergen, and Uwe Ligges. 2015. Nortest: Tests for Normality. Manual. https://doi.org/10.32614/CRAN.package.nortest.

Hochberg, Yosef, and Ajit C. Tamhane. 1987. Multiple Comparison Procedures. 1st ed. Wiley Series in Probability and Statistics. Wiley. https://doi.org/10.1002/9780470316672.

Hollander, Myles, Eric Chicken, and Douglas A. Wolfe. 2014. Nonparametric Statistical Methods. Third edition. Wiley Series in Probability and Statistics. Hoboken, New Jersey: John Wiley & Sons, Inc.

Holm, Sture. 1979. “A Simple Sequentially Rejective Multiple Test Procedure.” Scandinavian Journal of Statistics 6 (2): 65–70. https://www.jstor.org/stable/4615733.

Kozak, M., and H.-P. Piepho. 2018. “What’s Normal Anyway? Residual Plots Are More Telling Than Significance Tests When Checking ANOVA Assumptions.” J Agronomy Crop Science 204 (1): 86–98. https://doi.org/10.1111/jac.12220.

Kruskal, William H., and W. Allen Wallis. 1952. “Use of Ranks in One-Criterion Variance Analysis.” Journal of the American Statistical Association 47 (260): 583–621. https://doi.org/10.2307/2280779.

Kwak, Sang Gyu, and Jong Hae Kim. 2017. “Central Limit Theorem: The Cornerstone of Modern Statistics.” Korean J Anesthesiol 70 (2): 144–56. https://doi.org/10.4097/kjae.2017.70.2.144.

Levene, Howard. 1960. “Robust Tests for Equality of Variances.” In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling, edited by Ingram Olkin, 278–92. Stanford, CA: Stanford University Press.

Lumley, Thomas, Paula Diehr, Scott Emerson, and Lu Chen. 2002. “The Importance of the Normality Assumption in Large Public Health Data Sets.” Annu. Rev. Public Health 23 (1): 151–69. https://doi.org/10.1146/annurev.publhealth.23.100901.140546.

Mann, Henry B., and Donald R. Whitney. 1947. “On a Test of Whether One of Two Random Variables Is Stochastically Larger Than the Other.” The Annals of Mathematical Statistics 18 (1): 50–60. https://doi.org/10.1214/aoms/1177730491.

Moser, B K, and G. R. Stevens. 1992. “Homogeneity of Variance in the Two-Sample Means Test.” The American Statistician, February, 19–21. https://doi.org/10.1080/00031305.1992.10475839.

Olejnik, Stephen F., and James Algina. 1987. “Type I Error Rates and Power Estimates of Selected Parametric and Nonparametric Tests of Scale.” Journal of Educational Statistics 12 (1): 45. https://doi.org/10.2307/1164627.

Pearson, Karl. 1900. “On the Criterion That a Given System of Deviations from the Probable in the Case of a Correlated System of Variables Is Such That It Can Be Reasonably Supposed to Have Arisen from Random Sampling.” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 50 (302): 157–75. https://doi.org/10.1080/14786440009463897.

Rasch, Dieter, Klaus D. Kubinger, and Karl Moder. 2011. “The Two-Sample t Test: Pre-Testing Its Assumptions Does Not Pay Off.” Stat Papers 52 (1): 219–31. https://doi.org/10.1007/s00362-009-0224-x.

Razali, Nornadiah Mohd, and Yap Bee Wah. 2011. “Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests.” Journal of Statistical Modeling and Analytics 2 (1): 21–33.

Satterthwaite, F. E. 1946. “An Approximate Distribution of Estimates of Variance Components.” Biometrics Bulletin 2 (6): 110–14. https://doi.org/10.2307/3002019.

Searle, Shayle R. 1971. Linear Models. John Wiley & Sons.

SHAPIRO, S. S., and M. B. WILK. 1965. “An Analysis of Variance Test for Normality (Complete Samples).” Biometrika 52 (3-4): 591–611. https://doi.org/10.1093/biomet/52.3-4.591.

Shatz, Itamar. 2024. “Assumption-Checking Rather Than (Just) Testing: The Importance of Visualization and Effect Size in Statistical Diagnostics.” Behav Res 56 (2): 826–45. https://doi.org/10.3758/s13428-023-02072-x.

Šidák, Zbyněk. 1967. “Rectangular Confidence Regions for the Means of Multivariate Normal Distributions.” Journal of the American Statistical Association 62 (318): 626–33. https://doi.org/10.1080/01621459.1967.10482935.

Welch, B. L. 1947. “The Generalization of ‘Student’s’ Problem When Several Different Population Variances Are Involved.” Biometrika 34 (1–2): 28–35. https://doi.org/10.1093/biomet/34.1-2.28.

———. 1951. “On the Comparison of Several Mean Values: An Alternative Approach.” Biometrika 38 (3/4): 330–36. https://doi.org/10.2307/2332579.

Wilcox, Rand R. 2021. Introduction to Robust Estimation and Hypothesis Testing.

Yap, B. W., and C. H. Sim. 2011. “Comparisons of Various Types of Normality Tests.” Journal of Statistical Computation and Simulation 81 (12): 2141–55. https://doi.org/10.1080/00949655.2010.520163.

Yates, F. 1934. “Contingency Tables Involving Small Numbers and the $X$2 Test.” Journal of the Royal Statistical Society Series B: Statistical Methodology 1 (2): 217–35. https://doi.org/10.2307/2983604.